 |
Jeux des énigmes. Interdit aux crétins, donc que clode il reste dehors. =op [ Discussions générales, Duels, petits jeux rigolos... ]
retour forum
Pages : 1 - 2 - 3 - 4 - 5
| | | | | aah ? tu peux mettre ta solution, pasque ca ressemble pas trop au truc de Ob, moi. |
| | bens, 02.12.2003 à 12:57 | 125881 |
| | | | J'ai effectivement trouvé, et franchement merci Ob, c'est ton dessin qui m'a mis sur la voie (sérieusement en plus). |
| | bens, 02.12.2003 à 12:37 | 125875 |
| | | | J'ai pe trouvé, faut juste que je le prouve (à moi tout d'abord ;o)). En tout cas graphiquement ça a l'air juste... |
| | bens, 02.12.2003 à 12:34 | 125874 |
| | | Mort de rire.
Il a fallu qd même le message de Tini pour que je regarde encore sans me prendre la tête et que je comprenne... mais c'est pas de ma génération c'est pour ça ;o) |
| | | | | ah oui y'en a 2 possibles, ils se tracent de la meme facon, donc autant essayer de tracer le plus grand des 2, ya plus de place ;) |
| | Obion, 02.12.2003 à 12:27 | 125869 |
| | |  |
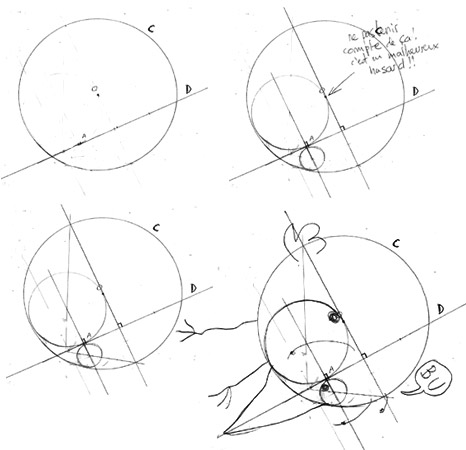| | Obion, 02.12.2003 à 12:09 | 125865 |
| | | | oui bens, ça c'est sur!! :)))) |
| | bens, 02.12.2003 à 12:08 | 125864 |
| | | | Trouver une droite où passe le(s) centre(s) est facile, trouver le(s) centre(s)... hum plus dur... |
| | cubik, 02.12.2003 à 12:03 | 125861 |
| | | | y a po du pythagore la dedans? |
| | bens, 02.12.2003 à 12:02 | 125859 |
| | | | Dans mes bras, Ob :o) |
| | bens, 02.12.2003 à 12:02 | 125858 |
| | | | Y'a 2 cercles passant par A et tangents à C et D. Les 2 peuvent être tracés de la même façon, ou non on doit en tracer un seul particulier ? |
| | Obion, 02.12.2003 à 12:01 | 125857 |
| | | | y a deux possibilités? |
| | | | ca veux dire que ca touche sans couper (et donc avec 1 seul point commun)
par exemple si on dessine une roue sur une route schematiquement ca donne un cercle tangeant a une droite |
| | | | | koiçaveut dire "tangeant"? |
| | | | allez je remonte ce surjet vieux de 6 mois pour un petit truc que j'ai eu a faire ce matin que j'ai un peu galeré dessus...
soit un cercle C de centre O, soit un point A dans se cercle et une droit D passant par A :
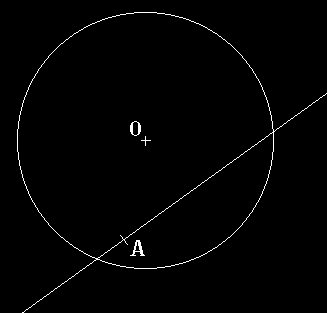
comment tracer avec une regle et un compa le cercle passant par A et tangeant a C et a D...
(ca a l'air facile mais c'est assez costaux en fait) |
| | bens, 08.06.2003 à 22:50 | 94432 |
| | | Il n'y a que des fous pour mettre une alarme sur une décapotable.
Vive les fous. |
| | Grunt, 08.06.2003 à 22:04 | 94426 |
| | | Ah oui. C'est pourri.
Mais ça m'éclate bien moi! =o)))) |
| | | | | en fait on me l'a deja raconté c'est tout pourrit, c'est une decapotable :o/ |
| | | | Bon, on va dire qu'il n'y a pas de vitres électricques mais mécaniques et qu'elles étaient fermées, sans traces d'effraction, et que ca existe bien des alarmes qui ne s'enclenchent que de l'intérieur (par exemple un truc à code et t'as pas de clavier sur ta commande à distance). Cherchez bien, quand on a la solution, c'est d'une simplicité rare.
A |
| | | | | si c'est des vitres electriques, il peux la fermer de l'exterieur. il appuis sur le bouton de fermeture et il retire son bras, la fitre fini de se fermer toute seule. |
| | J-C, 05.06.2003 à 8:45 | 94000 |
| | | une alarme que tu ne peux brancher que de l'intérieur de la voiture, ça n'existe pas !
At'chao ! |
| | Le PBE, 05.06.2003 à 8:39 | 93999 |
| | | | N'aurait-on pas trouvé le tueur avec le revolver dans la voiture (où il se serait enfermé après avoir commis son forfait, ne me demandez pas pourquoi) ? |
| | | | | Près d'une voiture, on trouve deux cadavres, tués par balles. On extrait les balles et analyse balistique et tout et tout. On retrouve le revolver dans la voiture. Les portes de la voiture sont fermées tout comme le coffre et le capot moteur. L'alarme est branchée, ce qu'on ne peut faire que de l'intérieur sur ce modèle, les vitres électricques sont fermées. Il n'y a aucun trou ni dans la carrosserie, complètement intacte, ni dans les vitres, ni dans le plancher. Comment le tueur a t'il fait ? |
| | bens, 04.06.2003 à 16:30 | 93918 |
| | | Ah oui Tini, je pensais pas aux personnes mortes. Sinon on n'a pas le droit de se serrer la main tout seul également, sinon ça marche pas non plus...
T'as trouvé bravo, avec une démonstration bien mathématique comme par hasard (mais bon, c'est juste au moins !! y'a un gars où je l'ai lu qui partait en live sur les maths, c'était long et la démo n'était même pas finie...).
Perso la démonstration que j'avais trouvée était la suivante:
"
Le nombre total de serrages de main est pair.
Ce nombre est égal aux mains serrées par ceux ayant serré un nombre pair de mains, ajoutées aux mains serrées par ceux ayant serré un nombre impair de mains. Le premier ensemble est pair, la somme est paire, et donc le 2ème ensemble est pair également.
Et si l'ensemble des mains serrées par ceux ayant serrés un nombre impair de mains est pair, c'est que nécessairement le nombre de ces personnes est un nombre pair.
"
|
| | | | | il est en train de mal tourner ce sujet... elles sont où les petites énigmes débiles niveau BAC -5 ? |
| | | | >> Aaaaaaaarg, 1 n'est pas premier !!!!
T'arrives un peu apres la bataille toi :o)
Bon, si on traduit ta definition en francais, ca donne qu'un nombre est compose si on peut l'ecrire comme un produit de 2 nombres tous les deux differents de 1, et premier si on ne peut pas. Ok, l'exclusion du 1 est un peu plus naturelle dans ce cas, puisque c'est directement relie a l'unicite de la decomposition en facteurs premiers.
C'est la vraie definition cette fois ? (je dis ca parce qu'on pourrait en trouver des douzaines qui sont equivalentes).
Pour les poignees de mains, je crois avoir trouve mais il faut ajouter juste une condition: on ne compte pas les poignees de mains qu'on a pu avoir avec des personnes mortes depuis.
Dans ce cas, le nombre est pair.
On appelle I l'ensemble des personnes qui ont serre la main a un nombre impair de personnes, et P l'ensemble des autres. Lorsque 2 personnes A et B se serrent la main, 3 cas peuvent se produire:
- A et B appartiennent a I: dans ce cas A et B passent de I dans P, donc #I (le nombre de personnes dans I) diminue de 2, et #P augmente de 2.
- A et B appartiennent a P: de meme, #I augmente de 2 et #P diminue de 2.
- A appartient a I et B a P (ou reciproquement): alors A passe dans P, et B dans I, donc #P et #I sont inchanges.
Une poignee de main de change donc pas la parite de I et P. Une personne qui nait est automatiquement dans P (elle n'a pas serre encore de main) donc I ne change pas, et une personne qui meurt revient a eliminer une poignee de main. A l'origine des temps, personne n'avait serre la main a personne, donc I etait vide (donc #I=0), et comme rien ne peut changer sa parite, #I reste pair. |
| | bens, 04.06.2003 à 1:13 | 93832 |
| | | Info pour ceux qui s'y intéressent, la petite automobile a rippé et inversé réductible et irréductible ds la 2ème étape.
Tiens, une énigme puisque c'est le sujet:
Dans le monde entier, le nombre de personnes ayant serré la main à un nombre impair de personnes, est-il pair ou impair ? (à démontrer également bien entendu, sinon c'est tout pourrite) |
| | boumbo, 03.06.2003 à 14:09 | 93739 |
| | | Les nombres premiers sont les irréductible positifs de Z (ensemble des entiers relatifs).
x est irréductible de Z si et seulement si il existe a et b dans Z non inversibles et non nuls tels que x=ab.
1 est inversible, il est même son propre inverse (1=1/1). Il n'est donc pas irréductible, il n'est donc pas premier. |
| | boumbo, 03.06.2003 à 13:57 | 93733 |
| | | | Aaaaaaaarg, 1 n'est pas premier !!!! |
| | | | | Ok, mais donnant donnant :o) |
| | | | | Heuuuu... juste pour dire à Tini qu'il devrait penser à fermer sa session quand il utilise mon ordi :o) |
| | ADDTC, 02.06.2003 à 18:30 | 93605 |
| | | >> En tout cas sa reponse vient de la, il avait juste garde le lien pour lui, le fourbe :o)
ADDTC fourbe, c'est un pléonasme ! Et puis je garde mes solutions pour moi, si je veux, non mais. |
| | | | | euh oui, la définition a certainement été adaptée avec tous ces théorèmes. Plutôt que de pondre une floppée de théorèmes disant "pour tout nombre premier strictement supérieur à 1", autant simplifier les théorèmes en postulant que 1 n'est pas premier. Ce qui a le bénéfice incomparable de pouvoir faire à l'occasion des théorèmes bonus qui marchent également avec 1 :o))) |
| | | | Qu'est-ce que tu fais dans ce sujet, Claude ? :o)
Sinon, moi ce qui m'intriguais c'est de savoir pourquoi on avait choisi par convention 1 non premier. En fait, c'est pas vraiment une histoire de nombre de diviseurs (meme si on peut choisir une definition ad hoc), mais plutot une histoire de commodite, car il y a plein de theoremes qui marchent pour n'importe quel nombre premier sauf 1. Du coup je me demandais si la definition du nombre premier ne se faisait pas plutot a l'aide d'un de ces theoremes. Mais en fait, non. |
| | | | | tout comme spirou, 2 et seulement 2 diviseurs, comme ça l'affaire est entendue :o))) |
| | | | Soit a appartenant à N
a est premier s'il admet exactement deux diviseurs: 1 et lui même (diviseur trivial).
1 n'est pas premier car il n'admet qu'un seul diviseur. |
| | | | Bien sur, mais tout ce que ca dit, c'est que:
n>=2 et n divisible seulement par 1 et par lui-meme => n premier.
Ca n'empecherait pas 1 d'etre premier. :o)
Mais bon, le sens de ma question c'etait plutot de savoir si 1 etait premier par convention, ou si la definition du nombre premier etait du style "degre de tout groupe cyclique qui blablabla", et qui eliminerait d'office 1. |
| | Le PBE, 02.06.2003 à 16:01 | 93586 |
| | | >>>Un nombre entier plus grand que UN est un nombre premier si ses seuls diviseurs sont 1 et lui-même.
Moi je comprends "strictement supérieur à 1" |
| | | | | Oui mais ca dit rien sur le statut de 1 ca. |
| | Le PBE, 02.06.2003 à 15:11 | 93578 |
| | | Sans chercher trop longtemps, on trouve cette définition:
Un nombre entier plus grand que UN est un nombre premier si ses seuls diviseurs sont 1 et lui-même.
|
| | | | En tout cas sa reponse vient de la, il avait juste garde le lien pour lui, le fourbe :o)
Quelle est la definition d'un nombre premier, au fait ? C'est "un nombre premier est un nombre qui n'est divisible que par 1 et par lui-meme, sauf 1 par convention" ou il y a une definition plus compliquee ? |
| | Le PBE, 02.06.2003 à 14:49 | 93574 |
| | | Addtc n'avait pas donné de démonstration, lui ;o)
J'ai moi aussi été surpris par cette limite de 20. A creuser.
Pour ta deuxième remarque, 1 n'est pas un nombre premier.
|
| | | | Je crois qu'addtc t'a précédé :o)
En fait c'est un probleme connu, je crois meme que c'est Martin Gardner qui l'a pose en premier.
Par contre il y a quelques trucs bizarres avec leur solution. J'ai l'impression qu'ils ont melange 2 versions du probleme, parce que sinon je ne vois pas d'ou sort cette limite de 20. Et surtout, il y a un truc que je ne comprends pas. Il se servent de la conjecture de Goldbach pour justifier que la somme ne peut pas etre paire.
En fait, la conjecture dit que tout nombre pair est la somme de 2 nombres premiers. Mais que se passe-t'il quand un de ces 2 nombres est 1 ? Imaginons qu'un nombre n pair soit la somme de n-1 et 1 premiers, et que cette decomposition soit la seule possible. Alors Stephane, s'il a comme somme n, peut en deduire que Pierre ne connait pas les 2 nombres, puisque il sait que ca ne peut pas etre 1. Et pourtant la somme est paire.
Je ne sais pas s'il existe une telle somme, mais en tout cas leur argument est un peu rapide.
|
| | Le PBE, 02.06.2003 à 14:10 | 93561 |
| | | | Je me suis mis tardivement au problème de Pierre et Stéphane. Alors que je cherchais des propriétés de la somme de deux nombres premiers (S ne peut pas pouvoir se décomposer comme l'addition de deux nombres premiers), je suis carrément tombé sur la solution, c'est ici. |
| | Obion, 29.05.2003 à 16:37 | 93001 |
| | | | mouais... |
| | | | nan c'etait pas un piege.
quand il pleut il a son parapluie, donc il peut atteindre le 10eme bouton :o) |
| | Obion, 28.05.2003 à 17:42 | 92956 |
| | | | c'était un piège matth??? |
| | Obion, 28.05.2003 à 17:33 | 92953 |
| | | ah... j'allais dire un truc mais avec l'indice de Matth ça ne colle pas trop... heu...
je tente quand même: s'il mesure un metre il ne peut pas atteindre les boutons au delà du 5? |
| | | | ah je la connais celle de kuk, je la laisse pour les autres...
j'ajoute juste que les jours de pluie il remonte jusqu'au 10eme directement par l'ascenseur |
| | Obion, 28.05.2003 à 17:30 | 92951 |
| | | | il voulait pas qu'on l'entende rentrer parce qu'il faisait l'école buissonnière? |
| | | | | Ben t'avais dit que 4 et 13 etaient solution, et effectivement on peut le verifier simplement. Par contre je ne vois pas de demonstration comme quoi c'est la seule. |
| | ADDTC, 28.05.2003 à 9:18 | 92842 |
| | | | Ha ! Je vous l'avais bien dit ! |
| | | | Alors, pour le problème du dialogue entre Pierre et Stéphane:
4 et 13 sont effectivement solution (ça on le savait déjà), mais c'est la seule (ça c'est nouveau). On peut le montrer avec une recherche exhaustive (un programme quoi), mais je ne sais pas s'il existe une démonstration plus élégante. Si vous avez des idées... |
| | Obion, 27.05.2003 à 18:49 | 92797 |
| | | il y a des énigmes qui ne marchent qu'à l'oral aussi parce qu'elles sont basées sur des jeux de mots.
et il y en a qui ne marchent qu'en anglais
enfin je dis ça... |
| | Obion, 27.05.2003 à 16:50 | 92786 |
| | | | je suis de l'avis d'ADDTC! c'est facile, je peux le faire aussi, c'est pas un super magicien! :o) |
| | ADDTC, 27.05.2003 à 14:35 | 92780 |
| | | Ben avant que le match commence, le score est de 0-0.
Enfin, normalement. Je pense. Quoique... |
| | | | | c'est des equipes d'hommes tronc ? |
| | | | | Un magicien annonce qu' il peut donner le score de n'importe quel match de water-polo juste avant qu' il ne commence. Il ne se trompe jamais, comment fait-il ? |
| | Obion, 24.05.2003 à 14:32 | 92329 |
| | | | :o| |
| | | | Il y avait 7 prêtres.
En effet, si un moine voit n autres rabbins avec des taches rouges sur le front, alors il va attendre jusqu'au (n+1)ème jour. Si les bonzes sont encore là, ça veut dire que eux voient aussi n taches, donc que lui-même est marqué du sceau de la malédiction. Il va donc se suicider le soir même, et comme tous les muezzins font le même raisonnement, ils meurent tous le même soir.
Les 7 abbés qui sont marqués voient 6 taches, et vont donc se suicider dimanche soir, alors que les sains, qui voient 7 taches, peuvent attendre jusqu'au lundi suivant. Le truc rigolo, c'est que si un mollah fait une blague en se peignant une fausse tache rouge sur le front, puis l'efface dimanche matin, alors tout le monastère se suicide :o) |
| | Grunt, 24.05.2003 à 14:06 | 92320 |
| | | >> hahaha... je n'ai pas la réponse mais on sent que Grunt a dù habilement (pfffhahaha) remplacer moines par curés et monastère par éclise parce qu'une connunauté de curés qui vit dans une église.....
>> quelle imagination pour contrer les google addicts! :o))
Moi qui voulait passer inaperçu. =o) |
| | | | | Des curés qui se suicident... c'est pas très catholique tout ça. |
| | Obion, 24.05.2003 à 13:12 | 92305 |
| | | | celle des tas de feuilles c'est pour Grunt! il faut bien qu'il en trouve au moins une quoi... :o)) |
| | Obion, 24.05.2003 à 13:11 | 92304 |
| | | :o))
ils avaient pas de nombril bernard et gilberte, c'est bien connu! :o) |
| | | | Des scientifiques ont découvert les corps de 2 personnes enfouies dans la neige du grand Nord. Ils sont très étonnés de l'incroyable état de conservation des corps, on aurait cru qu'ils étaient mort la veille! Et jusqu'à ce jour, ces scientifiques sont convaincus que ce sont là, les corps de Gilberte et Bernard... Comment est-ce possible ?
(dans l'énigme à la base c'était écrit Adam et Eve, j'ai changé le noms pour pas qu'on puisse chercher sur internet :o))) |
| | | | Un train électrique se déplace vers le sud-est à 90km/h, le vent souffle de l'ouest vers l'est à 30km/h. Dans quelle direction la fumée du train soufflera-t-elle ?
joli aussi celui là. |
| | | | Un super facile mais c'est tellement con que ça me fait rigoler comme énigme. Le genre d'énigme où le mec qui trouve pas a l'air terriblement bête.
Question : Deux hommes ratissent leurs jardins l'un fait 3 tas de feuilles et l'autre 7 lorsqu'ils mettront leurs tas en commun, combien de tas y aura-t-il ?
(réponse : kuk) |
| | | | | ah oui, on peut trouver sur google, j'avais même pas pensé à aller chercher... tian, je suis trop honnête des fois. bon, je dis pas la réponse. |
| | Obion, 24.05.2003 à 12:33 | 92294 |
| | | hahaha... je n'ai pas la réponse mais on sent que Grunt a dù habilement (pfffhahaha) remplacer moines par curés et monastère par éclise parce qu'une connunauté de curés qui vit dans une église.....
quelle imagination pour contrer les google addicts! :o)) |
Pages : 1 - 2 - 3 - 4 - 5 retour forum |
|
